Meep C-plus-plus Tutorial
From AbInitio
| Revision as of 19:18, 19 September 2008 (edit) Bermel (Talk | contribs) (added second compilation method for cpp files) ← Previous diff |
Revision as of 19:19, 19 September 2008 (edit) Bermel (Talk | contribs) (→Compiling) Next diff → |
||
| Line 282: | Line 282: | ||
| 1. After compiling the MEEP package following the instructions elsewhere in this wiki, place myfile.cpp (where myfile.cpp is a MEEP C++ file of your choosing) in the tests/ subdirectory, cd to the same directory, and type: | 1. After compiling the MEEP package following the instructions elsewhere in this wiki, place myfile.cpp (where myfile.cpp is a MEEP C++ file of your choosing) in the tests/ subdirectory, cd to the same directory, and type: | ||
| - | make myfile.dac | + | |
| + | make myfile.dac | ||
| + | |||
| The resulting executable may be invoked from the tests/ directory via: | The resulting executable may be invoked from the tests/ directory via: | ||
| - | ./myfile.dac | + | |
| + | ./myfile.dac | ||
| 2. Use the [[w:pkg-config]] program, which is installed by default on most GNU/Linux systems. Then, to compile a file <code>foo.cpp</code> using Meep, do: | 2. Use the [[w:pkg-config]] program, which is installed by default on most GNU/Linux systems. Then, to compile a file <code>foo.cpp</code> using Meep, do: | ||
Revision as of 19:19, 19 September 2008
| Meep |
| Download |
| Release notes |
| FAQ |
| Meep manual |
| Introduction |
| Installation |
| Tutorial |
| Reference |
| C++ Tutorial |
| C++ Reference |
| Acknowledgements |
| License and Copyright |
Instead of using the libctl/Scheme interface described in the Meep tutorial, one can also access Meep as a C++ library by writing a C++ program that links to it. The C++ interface provides the greatest level of flexibility in designing FDTD simulations.
(This is, in fact, the original way in which we used Meep, and the way in which all of the Meep test programs, in its tests/ directory, are written.)
We should also note that, while Meep is nominally in C++, it is perhaps better described as "C+". That is, most of the coding style is C-like with a few C++ features.
Contents |
Differences from libctl
The C++ interface has several differences from the libctl interface besides the obvious difference in syntax.
The most notable difference is that, while the libctl interface puts the origin (0,0,0) at the center of the computational cell, the C++ interface by default puts the origin at the corner of the computational cell. That is, an 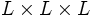 cell goes from ( − L / 2, − L / 2, − L / 2) to (L / 2,L / 2,L / 2) in libctl, but from (0,0,0) to (L,L,L) in C++. (You can change this by calling
cell goes from ( − L / 2, − L / 2, − L / 2) to (L / 2,L / 2,L / 2) in libctl, but from (0,0,0) to (L,L,L) in C++. (You can change this by calling volume::shift_origin.)
Overview
We begin with a very brief outline of a Meep C++ program, with minimal explanations, leaving more details for the examples below and the C++ reference page. Your C++ program should begin with:
#include <meep.hpp> using namespace meep;
to include the definitions of the Meep routines. Later, when you compile (see below), you must also link to the Meep libraries.
Your main program should then initialize Meep, and will generally then define a computational volume and the associated structure (describing the geometry and materials), initialize the fields, add sources, and then time-step. In short:
int main(int argc, char **argv) {
initialize mpi(argc, argv); // do this even for non-MPI Meep
double resolution = 20; // pixels per distance
volume v = vol2d(5,10, resolution); // 5x10 2d cell
structure s(v, eps, pml(1.0));
fields f(&s);
f.output_hdf5(Dielectric, v.surroundings());
double freq = 0.3, fwidth = 0.1;
gaussian_src_time src(freq, fwidth);
f.add_point_source(Ey, src, vec(1.1, 2.3));
while (f.time() < f.last_source_time()) {
f.step();
}
f.output_hdf5(Hz, v.surroundings());
return 0;
}
This example, doesn't do much — it just runs a Gaussian source and outputs the 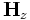 field at the end. The dielectric structure is determined by the user-defined function
field at the end. The dielectric structure is determined by the user-defined function eps, which has the form:
double eps(const vec &p) {
if (p.x() < 2 && p.y() < 3)
return 12.0;
return 1.0;
}
which returns the dielectric function 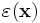 (here, just a 2×3 rectangle of ε=12 in the upper-left corner). Unlike in the libctl front-end, by default the origin 0 of the coordinate system is at the corner of the computational cell.
(here, just a 2×3 rectangle of ε=12 in the upper-left corner). Unlike in the libctl front-end, by default the origin 0 of the coordinate system is at the corner of the computational cell.
Now that you have the basic flavor, we can proceed to some more specific examples.
Computing the Quality Factor of a Resonator
In this first tutorial, we will write the script to compute the quality factor of a 1D Fabry-Perot cavity. For a 1D system, Meep considers a computational cell along the z coordinate. The control file will be a C++ file (having extension *.cpp). In order to use all the classes and subroutines available in Meep, the first two lines of any control file must be the following:
#include <meep.hpp> using namespace meep;
The particular Fabry-Perot cavity we will investigate consists of an air region bounded by two distributed Bragg reflectors (quarter-wave stack) of epsilon 12 and 1. We choose the size of the defect to be twice as large as the air thickness in the quarter-wave stack, so that a defect mode is found near midgap. This structure will include N = 5 periods in the Bragg reflector on either side of the defect. We can use a larger N but the quality factor may then be too large to compute. The parameters are set up as follows:
const double eps1 = 12.0; // epsilon of layer 1 const double eps2 = 1.0; // epsilon of layer 2 const double grating_periodicity = 1.0; const double d1 = sqrt(eps2) / (sqrt(eps1)+sqrt(eps2)); // quarter wave stack dimensions const double d2 = sqrt(eps1) / (sqrt(eps1)+sqrt(eps2)); const double half_cavity_width = d2; const int N = 5;
Meep supports perfectly matching layers (PML) as absorbing boundary conditions. The PML begins at the edge of the computational volume and works inwards. Hence, we specify the size of the computational cell as follows (note that z_center is half the cell length):
const double pml_thickness = 1.0; const double z_center = half_cavity_width + N*grating_periodicity + pml_thickness;
To specify a dielectric structure in Meep, we define a function that takes as input one parameter, a position vector, and returns the value of the dielectric at that position.
double eps(const vec &p) {
vec r = p - vec(z_center);
if (abs(r.z()) < half_cavity_width)
return 1.0;
else {
double dz = abs(r.z()) - half_cavity_width;
while (dz > grating_periodicity)
dz -= grating_periodicity;
return (dz < d1) ? eps1 : eps2;
}
}
We are now ready to set up the computational cell, excite the sources, time step the fields, and compute the resulting quality factor. Here we set up the main part of the control file incorporating some of Meep's classes and sub routines. We will excite the mode at the midgap of the bandgap, which we expect to have the largest quality factor since it will have the largest exponential decay.
int main(int argc, char **argv){
initialize mpi(argc,argv);
const double amicron = 10.0;
const volume vol = vol1d(2*z_center,amicron);
structure s(vol,eps,pml(pml_thickness));
fields f(&s);
Note the constructor for the volume class in 1D which takes as parameters the size of the cell and the resolution. The sources in Meep are excitations of the polarization vector in 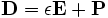 . The polarization can be any one of the six cartesian or cylindrical fields. There are a variety of sources including dipole and current sources, gaussian pulses and a continuous wave sources. For now, we use a gaussian source centered at the midgap frequency with a narrow width, along with the start time and end time of the source.
. The polarization can be any one of the six cartesian or cylindrical fields. There are a variety of sources including dipole and current sources, gaussian pulses and a continuous wave sources. For now, we use a gaussian source centered at the midgap frequency with a narrow width, along with the start time and end time of the source.
const double w_midgap = (sqrt(eps1)+sqrt(eps2))/(4*sqrt(eps1)*sqrt(eps2)); gaussian_src_time src(w_midgap, 1.0, 0.0, 5.0); f.add_point_source(Ex, src, vol.center());
Here we make use of the built in function, vol.center(), that automatically computes the geometric center of the of the computational volume. To see what the unit cell of the dielectric function looks, output as an HDF5 file, we invoke the built in command:
f.output_hdf5(Dielectric, v.surroundings())
This versatile command can be used to visualize all of the field components, field energy when called at a particular time step. The resulting output file will be eps-000000.00.h5 and to view it, we first need to convert it to the portable network graphics (PNG) format with the h5topng tool. We are now ready to begin the time stepping of the fields, and do so in a simple loop:
while (f.time() < f.last_source_time()) f.step();
To calculate the quality factor, we need to monitor a field beyond the time at which our point source has been turned off. We can do this in Meep by establishing an array where all fields at a particular point can be monitored. We set up the area as well as the output arrays we will need later as such:
int maxbands = 5; int ttot = int(400/f.dt)+1; complex<double> *p = new complex<double>[ttot]; complex<double> *amps = new complex<double>[maxbands]; double *freq_re = new double[maxbands]; double *freq_im = new double[maxbands];
The variable maxbands is the number of mode frequencies we will be looking for while ttot represents the total number of timesteps for which we will monitor the field component at. For this simulation given the large quality factor that we expect, we will time step for a long period of time which in this case is 400 unit seconds. Now we are ready to time step and collect the field information:
int i=0;
while (f.time() < f.last_source_time() + 400) {
f.step();
p[i++] = f.get_field(Ex,vol.center());
}
The get_field function does exactly that, obtains the value of the field at a given position within the computational cell using linear interpolation where necessary. Now we have all the information we need and must obtain the frequencies of the modes which we do by invoking a special tool for harmonic inversion, harminv, to extract the real and imaginary frequencies:
int num = do_harminv(p, ttot, f.dt, 0.8*w_midgap, 1.2*w_midgap, maxbands, amps, freq_re, freq_im);
The integer returned by harminv is the number of mode frequencies obtained from the input data p. The particular call to harminv included passing the arrays by value and telling harminv to look for frequencies within 20% of the mid gap frequency up to a maximum of 5 bands. At this point, the necessary information to compute the quality has been stored in the freq_re and freq_im arrays and we compute the quality factor using the formula, Q = − ωr / 2ωi. All that is left to do, is to print these results with the quality factor:
master_printf("frequency,amplitude,quality factor\n");
for (int i=0; i<num; ++i)
master_printf("%0.6g%+0.6gi,%0.5g%+0.5gi,%g\n",freq_re[i],freq_im[i],real(amps[i]),imag(amps[i]),-0.5*freq_re[i]/freq_im[i]);
return 0;
}
That's it, we are done. The output for this program is 3.26087e+06. The large quality factor is to be expected since our system includes a relatively high number of bragg reflectors (N=5) in each direction and we are exciting the mode at mid gap. Suppose we want to see what the resonant mode looks like, say over one period. The following block of code time steps the field for exactly one period while outputting the Ex field for the computational cell at each time step:
double curr_time = f.time();
while (f.time() < curr_time + 1/w_midgap) {
f.output_hdf5(Ex, vol.surroundings());
f.step();
}
After we convert the hdf5 files to PNG format and superimpose the images on the dielectric background to produce an animated, we obtain the following:
Calculating the flux through a close packed opal monolayer
In this example, we will look at a system that is a bit more computationally expensive: a 3D structure consisting of a close packed monolayer of silica opal spheres on a silicon substrate in an environment of air. We want to determine what the transmission spectrum is for such a structure over the visible frequency range between 400nm to 900nm normally incident on the monolayer. Our structure will include silica opal spheres having a diameter of 850nm. As usual, we begin with the header information for a MEEP control file:
#include "meep.hpp" using namespace meep;
The 3D unit cell is a rectangular box consisting of the opal monolayer in the middle surrounded by air and silicon. In the middle of the unit cell where the rectangular XY plane bisects the monolayer of opal spheres, 3 spheres touch along the main diagonal giving rise to the formula 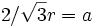 . We arbitrarily choose a lattice constant of one in the y-direction, and so our normalized radius is:
. We arbitrarily choose a lattice constant of one in the y-direction, and so our normalized radius is:
const double rad = 1/(2*sqrt(3));
This means that our computational cell is 2r units in size in the X direction. This simulation will make use of a planar gaussian excitation, for which the amplitude of the field is specfieid at each position in the plane via a function which in our case will be constant everywhere in the plane:
complex<double> one(const vec &p) {
return 1.0;
}
When computing transmission through a given structure, we always need to normalize by the transmission through an empty structure. As a result, the empty dielectric function is:
double empty(const vec &p) {
return 1.0;
}
Now we need to define the dielectric function for our structure involving the monolayer of silica opal spheres. We break up the structure into three main regions, the top of the structure includes just air, the monolayer in the middle, and the glass substrate beneath.
double monolayer(const vec &p) {
const volume v = vol3d(0.6,1.0,6.0,100);
vec xx = p - v.center();
We fist check to see whether the Z location of the position vector is beyond the height of the spheres and return air if it is:
if (xx.z() > rad+1e-06) return 1.0;
Otherwise, we check to see whether we are below the monolayer and return glass:
else if (xx.z() < -rad-1e-06) return 2.25;
Having eliminated the previous two cases, we thus determine that the position vector p is located somewhere within the monolayer of silica opal spheres. Prior to checking to see whether the position vector is located within one of the spheres of the unit cell, we first translate the position vector into the 2D unit cell, centered at the monolayer:
while (xx.x() > 0.3) xx -= vec(0.6,0); while (xx.y() > 0.5) xx -= vec(0,1.0); while (xx.x() < -0.3) xx += vec(0.6,0); while (xx.y() < -0.5) xx += vec(0,1.0);
The basis vectors for the close packed monolayer are (r,r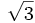 ) and (2r,0). Starting from the center of the cell, we shift by several linear combination of the lattice vectors and check to see whether the current position is located within a circle centered at these locations. If it is, we return the dielectric of silica and if after having looped through all the lattice locations we have not found a match, we return air.
) and (2r,0). Starting from the center of the cell, we shift by several linear combination of the lattice vectors and check to see whether the current position is located within a circle centered at these locations. If it is, we return the dielectric of silica and if after having looped through all the lattice locations we have not found a match, we return air.
vec b1(0.3,0.52,0), b2(0.6,0,0);
for (int j=-1; j<=1; ++j)
for (int k=-1; k<=1; ++k)
if (sqrt((xx-b1*j-b2*k)&(xx-b1*j-b2*k)) < rad+1e-06)
return 2.25;
return 1.0;
}
The 2D cross-section of the middle of the 3D unit cell, showing the close packed opal spheres can be seen in the image.
Having defined the dielectric functions, we are ready to create the computational cell, establish the volume sources, time step the fields and compute the transmission spectrum.
void excitefilm(double a, component c) {
volume v = vol3d(0.6,1.0,6.0,a);
We create two separate structures and fields to include the empty structure and one including the opal monolayer.
structure s0(v,empty,pml(0.5,Z)); structure s(v,monolayer,pml(0.5,Z)); fields f0(&s0); fields f(&s); f0.use_bloch(vec(0,0,0)); f.use_bloch(vec(0,0,0));
Remembering that Meep uses normalized units of frequency, the frequencies corresponding to 400nm and 900nm wavelengths are:
double freq_min = 0.34, freq_max = 2.125; int nfreq = 500; gaussian_src_time src((freq_min+freq_max)*0.5, 0.5/(freq_max-freq_min), 0, 5/(freq_max-freq_min));
The source plane and flux plane are positioned at the top and bottom of the computational cell respectively.
geometric_volume src_plane(vec(0,0,5.0),vec(0.6,1.0,5.0));
geometric_volume flux_plane(vec(0,0,1.0),vec(0.6,1.0,1.0));
f0.add_volume_source(c,src,src_plane,one,1.0);
f.add_volume_source(c,src,src_plane,one,1.0);
master_printf("volume sources added...\n");
dft_flux ft0 = f0.add_dft_flux_plane(flux_plane,freq_min,freq_max,nfreq);
dft_flux ft = f.add_dft_flux_plane(flux_plane,freq_min,freq_max,nfreq);
master_printf("simulating empty structure...\n");
while (f0.time() < nfreq / (freq_max-freq_min) / 2) f0.step();
ft -= ft0;
master_printf("simulating silica opal monolayer...\n");
while (f.time() < nfreq / (freq_max-freq_min) / 2) f.step();
double *flux = ft.flux();
double *flux0 = ft0.flux();
Finally, we normalize the flux and output the transmission spectrum.
double *T;
T = new double[nfreq];
for (int i=0; i<nfreq; ++i)
T[i] = flux[i] / flux0[i];
double dfreq = (freq_max-freq_min) / (nfreq-1);
master_printf("tranmission:, freq, T[i]\n");
for (int i=0; i<nfreq; ++i)
master_printf("transmission:, %f, %f\n",freq_min+i*dfreq,T[i]);
delete [] flux;
delete [] flux0;
}
The main part of the program then calls the excitefilm procedure with a resolution of 40 pixels per a to compute the transmission flux.
int main(int argc, char **argv) {
initialize mpi(argc, argv);
master_printf("beginning silica opal transmission tests...\n");
excitefilm(40, Ey);
master_printf("finished.\n");
return 0;
}
Compiling
In order to compile your code and link against the Meep library, you must link in several additional libraries that Meep requires. There are two ways to do this:
1. After compiling the MEEP package following the instructions elsewhere in this wiki, place myfile.cpp (where myfile.cpp is a MEEP C++ file of your choosing) in the tests/ subdirectory, cd to the same directory, and type:
make myfile.dac
The resulting executable may be invoked from the tests/ directory via:
./myfile.dac
2. Use the w:pkg-config program, which is installed by default on most GNU/Linux systems. Then, to compile a file foo.cpp using Meep, do:
g++ `pkg-config --cflags meep` foo.cpp -o foo `pkg-config --libs meep`
(Naturally, replace g++ with the name of your C++ compiler if you are not using the GNU compilers.)


